Use Gram-schmidt to Find Orthonormal Basis
Homework Equations Gram-Schmidt equations The Attempt at a Solution I did the problem. Allow v 1v k to be a non-orthonormal basis for V.

Use The Gram Schmidt Process To Find The Orthonormal Basis For The Row Space Of The Matrix A R Maths
The resulting orthogonal set v1 v2 vn consists of n linearly independent vectors in V and so forms an orthogonal basis for V.

. What is Gram Schmidt Orthonormalization Process. V1 x1 122 v2 x2 hx2v1i hv1v1i v1 102 3 9 122 432343 v3 x3 hx3v1i hv1v1i v1 hx3v2i hv2v2i v2 001 2 9 122 43 4 432343 292919. A Find an orthonormal basis of the plane x y z 0 and form the projection matrix P QQT.
Which is an orthonormal basis in the Gram-Schmidt method. Just replace all u cdot v with. 2 6 6 4 2 2 4 2 3 7 7 5.
2 6 6 4 1 1 0 0 3 7 7 5gand then write down the QR decomposition. That simplifies the calculation. Take u₂ v₂ - v₂ u₁ u₁ u₁ u₁ and set e₂ 1 u₂ u₂.
Then simply normalize each vector in the basis. Free Gram-Schmidt Calculator - Orthonormalize sets of vectors using the Gram-Schmidt process step by step This website uses cookies to ensure you get the best experience. Matrix then the rows of M form an orthonormal basis for Rn and the columns of M form an orthonormal basis for Rn.
Homework Statement Find orthonormal basis for 1 x x2 from -1 to 1. Use the Gram-Schmidt process to produce an orthogonal basis for W. Usually its easier to normalize after having applied the Gram-Schmidt algorithm.
Use Gram-Schmidt to find an orthonormal basis for the space spanned by. Who are the experts. Orthonormal bases and Gram-Schmidt process.
Well build u 1u k repeatedly until u 1u p is an orthonormal basis for the span of v 1v p. Ad Over 27000 video lessons and other resources youre guaranteed to find what you need. Using the Gram-Schmidt process we orthogonalize the basis x1 122 x2 102 x3 001.
The method for finding the second vector is to take the projection of the x 2 on v 1. We came up with a process for generating an orthonormal basis in the last video and it wasnt a new discovery. A 202 412 B 1001 0.
The first vector can remain the same making v 1 0 8 8. Q1 Use Gram-Schmidt orthonormalization process to transform the basis B 100 11 1 1 1 1 for R into an orthonormal basis. Determine whether this is the case in your software.
Richard Anstee Consider a vector space V with an inner product. Take vectors v₁ v₂ v₃ vₙ whose orthonormal basis youd like to find. Can someone review and explain where I went wrong.
But lets apply that now to some real examples and hopefully well see that its a lot more concrete than it might have looked in the last video. First find an orthogonal basis then normalize it and you have an orthonormal basis. My attempt is attached.
Let V be a k-dimensional subspace of R n. Lets do one more Gram-Schmidt example. By using this website you agree to our Cookie Policy.
Use the Gram-Schmidt orthogonalization process to find an orthonormal. If it is compare your softwares output with the solution given in Example. View gram-schmpdf from MATH 70 at Tufts University.
To obtain an orthonormal basis which is an orthogonal set in which each vector has norm 1 for an inner product space V use the Gram-Schmidt algorithm to construct an orthogonal basis. Basis for the subspace W of R4 spanned by S v1 v2 v3 1111 3212 1230. Using Gram-Schmidt orthogonalization find an orthogonal basis for the span of the vectors mathbfw_1mathbfw_2inR3 if mathbfw_1 beginbmatrix 1 0 3 endbmatrixquad mathbfw_2 beginbmatrix 2 -1 0 endbmatrix.
With this we can rewrite the Gram-Schmidt process in a way that would make mathematicians nod and grunt their approval. Perform the Gram-Schmidt process on the three vectors f 2 6 6 4 5 5 5 5 3 7 7 5. Take u₁ v₁ and set e₁ 1 u₁ u₁.
So lets say I have the subspace V that is spanned by the vectors-- lets say were dealing in R4 so the first vector is 0 0 1 1. It would be much appreciated. To obtain an orthonormal basis which is an orthogonal set in which each vector has norm 1 for an inner product space V use the Gram-Schmidt algorithm.
Use the Gram-Schmidt process to find an orthonormal basis for the subspace Use the Gram-Schmidt process to find an orthonormal basis for the subspace of R4 with basis. Begin with any basis for V we look at how to get an orthonormal basis for V. And then a third vector-- so its a three-dimensional subspace of R4-- its 1 1 0 0 just like that three-dimensional.
The second vector is 0 1 1 0. Example Using the orthonormal basis from 1 we obtain M 2 6 4 1 p 3 0 2 p 6 1 p 3 1 p 2 1 p 6 1 p. Begingroup You can apply the Gram-Schmidt process with any inner product.
Lets say I have the plane x1 plus x2 plus x3 is. The given set is a basis for subset W. Experts are tested by Chegg as specialists in their subject area.
Its called the Gram-Schmidt process. B Find an orthonormal basis of the hyper plane x 1 x 2 x 3 x 4 x 5 0 in R5. Coefficient matrix is not square or is nonsingular.
Add to solve later. We review their content and use your feedback to keep the. 0 8 8 4 7 3 The Gram-Schmidt process is a method of turning a basis x 1 x 2 into an orthogonal basis v 1 v 2.
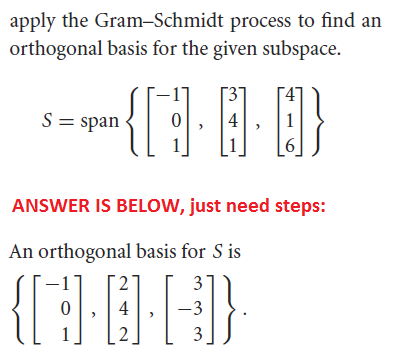
Solved Apply The Gram Schmidt Process To Find An Orthogonal Chegg Com
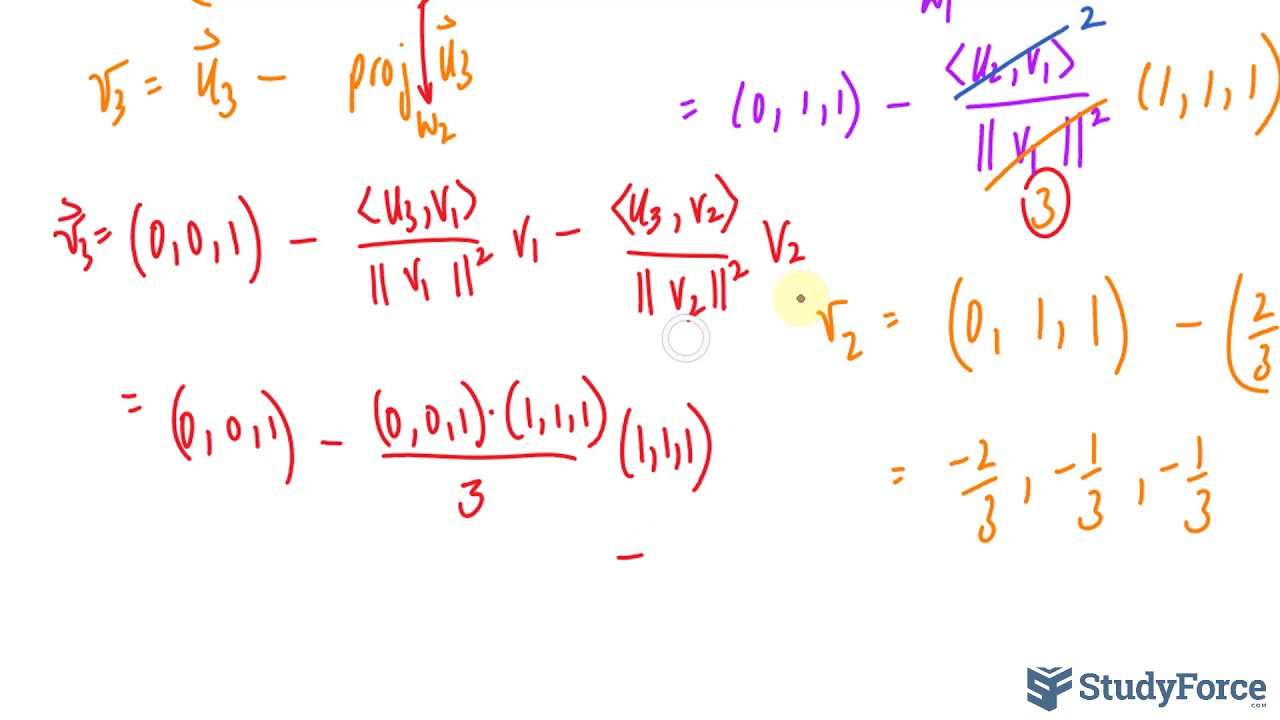
Use The Gram Schmidt Process To Find An Orthonormal Basis Youtube

Obtaining Orthogonal Basis Using The Gram Schmidt Process Math Tricks Mathematics Fun Math
No comments for "Use Gram-schmidt to Find Orthonormal Basis"
Post a Comment